Arc Length Calculator
How to use this Arc Length Calculator 🤔
- Enter ✎ value for radius (r).
- Enter ✎ value for angle (θ).
- As soon as you enter the required input value(s), the Arc Length is calculated immediately, and displaed in the output section (present under input section).
Calculation
Once you enter the input values in the calculator, the output parameters are calculated.
Examples
The following examples cover how to calcualte the Arc Length when radius, and angle are given.
1. What is the Arc Length of Sector whose radius is 10 units, and angle is 180 degrees?
Answer
Given:
- radius, r = 10 units
- angle, θ = 180 degrees
The formula to find the Arc Length of a Sector is:
l = \( r θ \frac{\pi}{180} \)
Substitute given values in the above formula.
l = \(10\times180\times \frac{\pi}{180} \)
l = 31.42 units
∴ Arc Length, l = 31.42 units
2. What is the Arc Length of Sector whose radius is 2 units, and angle is 45 degrees?
Answer
Given:
- radius, r = 2 units
- angle, θ = 45 degrees
The formula to find the Arc Length of a Sector is:
l = \( r θ \frac{\pi}{180} \)
Substitute given values in the above formula.
l = \(2\times45\times \frac{\pi}{180} \)
l = 1.57 units
∴ Arc Length, l = 1.57 units
{
"topic": "arc-length",
"img": {
"width": 230,
"height": 260
},
"input_types": [
"float",
"float"
],
"input_labels": [
"r",
"θ"
],
"input_values": [
"8",
"60"
],
"input_units": [
"units",
"degrees"
],
"input_descriptions": [
"radius",
"angle"
],
"examples": [
{
"r": 10,
"θ": 180
},
{
"r": 2,
"θ": 45
}
],
"type": "Calculate",
"title": "Arc Length",
"category": "Geometry",
"shape": "Sector",
"formula": " r * θ * ( Math.PI / 180 ) ",
"formula_mathjax": "\\( r θ \\frac{\\pi}{180} \\)",
"formula_mathjax_sub": "\\( r \\times θ \\times \\frac{\\pi}{180} \\)",
"op_label": "Arc Length",
"output_unit": "units",
"description": "The arc length calculator calculates the length of arc of a sector by taking its radius and sector angle as inputs.",
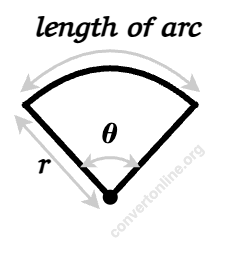
"explanation": "In a sector, the length of arc is distance on the sector that is the part of the circumference of the respective circle.",
"examples_data": "<h2>Examples</h2><p>The following examples cover how to calcualte the Arc Length when radius, and angle are given.</p><div class=\"example\"><h3 class=\"question\"><span class=\"example_n\">1.</span> What is the Arc Length of Sector whose radius is 10 units, and angle is 180 degrees?</h3><h4 class=\"answer\">Answer</h4><p>Given:</p><ul><li>radius, r = 10 units<li>angle, θ = 180 degrees</ul><p>The formula to find the Arc Length of a Sector is:</p><p class=\"tabspace\">l = \\( r θ \\frac{\\pi}{180} \\)</p><p>Substitute given values in the above formula.</p><p class=\"tabspace\">l = \\(10\\times180\\times \\frac{\\pi}{180} \\)</p><p class=\"tabspace\">l = 31.42 units</p><p class=\"tabspace answer\">∴ Arc Length, l = 31.42 units</p></div><div class=\"example\"><h3 class=\"question\"><span class=\"example_n\">2.</span> What is the Arc Length of Sector whose radius is 2 units, and angle is 45 degrees?</h3><h4 class=\"answer\">Answer</h4><p>Given:</p><ul><li>radius, r = 2 units<li>angle, θ = 45 degrees</ul><p>The formula to find the Arc Length of a Sector is:</p><p class=\"tabspace\">l = \\( r θ \\frac{\\pi}{180} \\)</p><p>Substitute given values in the above formula.</p><p class=\"tabspace\">l = \\(2\\times45\\times \\frac{\\pi}{180} \\)</p><p class=\"tabspace\">l = 1.57 units</p><p class=\"tabspace answer\">∴ Arc Length, l = 1.57 units</p></div>",
"schema_data": "\n <script type=\"application/ld+json\">\n {\n \"@context\": \"https://schema.org\",\n \"@type\": \"Article\",\n \"author\": {\n \"@type\": \"Person\",\n \"name\": \"Mallikarjuna M\",\n \"honorificSuffix\": \"B.Tech. (Electronics & Communication)\",\n \"url\": \"https://www.linkedin.com/in/mallikarjuna-mallisetty-7330314a/\"\n },\n \"image\": [\"https://convertonline.org/images/calculators/arc-length.png\"],\n \"dateModified\": \"2024-09-05T00:23:14.014Z\",\n \"datePublished\": \"2024-07-21T07:20:32.526Z\",\n \"description\": \"The arc length calculator calculates the length of arc of a sector by taking its radius and sector angle as inputs.\",\n \"headline\": \"Arc Length Calculator\",\n \"mainEntityOfPage\": {\n \"@id\": \"https://convertonline.org\",\n \"@type\": \"WebPage\"\n },\n \"publisher\": {\n \"@type\": \"Organization\",\n \"name\": \"ConvertOnline.org\",\n \"logo\": {\n \"@type\": \"ImageObject\",\n \"url\": \"https://convertonline.org/images/icon.png\",\n \"width\": \"512px\",\n \"height\": \"512px\"\n }\n }\n }\n </script>\n "
}
ConvertOnline