csc Calculator
θ angle
csc(θ)
Calculating Cosecant of an Angle
The cosecant (cosec) of an angle in a right-angled triangle is a trigonometric function that represents the ratio of the length of the hypotenuse to the opposite side. The cosecant function is the reciprocal of the sine function and is commonly used in trigonometric calculations.
The cosecant of an angle \( \theta \) is defined as:
\( cosec(\theta) = \dfrac{\text{length of hypotenuse}}{\text{length of opposite side}} \)
where:
- hypotenuse is the side opposite to the right angle.
- opposite side is the side opposite to angle \( \theta \).
Consider the following triangle ABC, right-angled at vertex B.
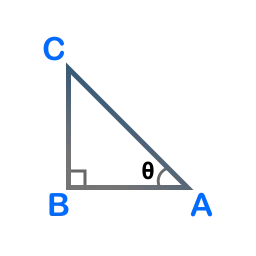
For the angle \( \theta \) at vertex A:
- Hypotenuse = AC
- Opposite side = BC
Therefore,
\( cosec(\theta) = \dfrac{\text{length of side AC}}{\text{length of side BC}} \)
Examples
The following examples demonstrate how to use the cosecant of an angle to find the length of the hypotenuse or the opposite side in various practical situations.
1. What is the cosecant of an angle θ if the length of the hypotenuse is 5 units and the length of the opposite side is 3 units?
Answer
Given:
- Length of the hypotenuse = 5 units
- Length of the opposite side = 3 units
The formula to calculate the cosecant of an angle θ is:
\( cosec(\theta) = \dfrac{\text{length of hypotenuse}}{\text{length of opposite side}} \)
Substitute the given values into the formula:
\( cosec(\theta) = \dfrac{5}{3} \)
Simplify the expression:
\( cosec(\theta) \approx 1.67 \)
∴ cosec(θ) ≈ 1.67
2. A person is flying a kite at an angle of 30° to the horizontal. If the height of the kite above the ground is 20 meters, how long is the string of the kite?
Answer
Given:
- Height of the kite (opposite side) = 20 meters
- Angle with the horizontal θ = 30°
Using the cosecant function to find the length of the string (hypotenuse):
\( cosec(30°) = \dfrac{\text{length of string}}{20} \)
Simplify the expression:
\( 2 = \dfrac{\text{length of string}}{20} \)
Now solve for the length of the string:
\( \text{Length of string} = 2 \times 20 = 40 \text{ meters} \)
∴ The length of the kite's string is 40 meters.
3. A ladder is leaning against a wall, making a 45° angle with the ground. If the length of the ladder is 10 meters, how far is the top of the ladder from the ground?
Answer
Given:
- Length of the ladder (hypotenuse) = 10 meters
- Angle with the ground θ = 45°
Using the cosecant function to find the height from the ground (opposite side):
\( cosec(45°) = \dfrac{10}{\text{height from ground}} \)
Simplify the expression:
\( 1.414 = \dfrac{10}{\text{height from ground}} \)
Now solve for the height from the ground:
\( \text{Height from ground} = \dfrac{10}{1.414} \approx 7.07 \text{ meters} \)
∴ The top of the ladder is approximately 7.07 meters from the ground.
4. A cable is attached to the top of a 50-meter-high tower and is secured to the ground. If the angle between the cable and the ground is 60°, what is the length of the cable?
Answer
Given:
- Height of the tower (opposite side) = 50 meters
- Angle with the ground θ = 60°
Using the cosecant function to find the length of the cable (hypotenuse):
\( cosec(60°) = \dfrac{\text{length of cable}}{50} \)
Simplify the expression:
\( 1.154 = \dfrac{\text{length of cable}}{50} \)
Now solve for the length of the cable:
\( \text{Length of cable} = 1.154 \times 50 \approx 57.7 \text{ meters} \)
∴ The length of the cable is approximately 57.7 meters.