sin−1 Calculator
x= opposite_side/hypotenuse
sin−1(x)
Calculating Inverse Sine of a Value
The inverse sine (sin⁻¹) function, also known as arcsine, is used to find the angle whose sine is a given value. This function is particularly useful in trigonometry when you need to determine the angle based on the ratio of the opposite side to the hypotenuse in a right-angled triangle.
The inverse sine of a value \( x \) is defined as:
\( \theta = \sin^{-1}(x) \)
where:
- θ is the angle corresponding to the sine value.
- x is the sine value, representing the ratio of the opposite side to the hypotenuse.
Consider the following triangle ABC, right-angled at vertex B.
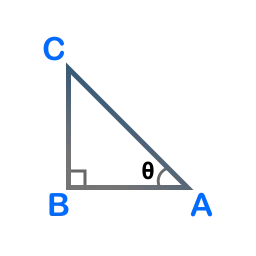
For the angle \( \theta \) at vertex A:
- Opposite side = BC
- Hypotenuse = AC
Therefore,
\( \sin^{-1}(x) = \theta \) where \( x = \dfrac{\text{length of side BC}}{\text{length of side AC}} \)
Examples
The following examples demonstrate how to use the inverse sine function to find the angle when the sine value is known.
1. A painter's ladder is 12 feet long and reaches 9 feet high against a wall. What is the angle that the ladder makes with the ground?
Answer
Given:
- Length of the hypotenuse (ladder) = 12 feet
- Length of the adjacent side (height) = 9 feet
First, calculate the sine of the angle:
\( \sin(\theta) = \dfrac{\text{height}}{\text{length of ladder}} = \dfrac{9}{12} \)
Simplify the expression:
\( \sin(\theta) = 0.75 \)
Now, find the angle using the inverse sine function:
\( \theta = \sin^{-1}(0.75) \)
Using a calculator or reference table, the angle is:
∴ θ ≈ 48.6°
2. A hiker is standing at the base of a hill. If the distance to the top of the hill along the slope is 100 meters, and the height of the hill is 80 meters, what is the angle of elevation?
Answer
Given:
- Length of the hypotenuse (slope) = 100 meters
- Length of the adjacent side (height) = 80 meters
First, calculate the sine of the angle:
\( \sin(\theta) = \dfrac{\text{height}}{\text{length of slope}} = \dfrac{80}{100} \)
Simplify the expression:
\( \sin(\theta) = 0.8 \)
Now, find the angle using the inverse sine function:
\( \theta = \sin^{-1}(0.8) \)
Using a calculator or reference table, the angle is:
∴ θ ≈ 53.1°
3. A flagpole casts a shadow 15 meters long on the ground. If the distance from the top of the flagpole to the tip of the shadow is 25 meters, what is the angle of elevation of the sun?
Answer
Given:
- Length of the hypotenuse (distance from the top of the flagpole to the tip of the shadow) = 25 meters
- Length of the adjacent side (shadow length) = 15 meters
First, calculate the sine of the angle:
\( \sin(\theta) = \dfrac{\text{shadow length}}{\text{distance from the top of the flagpole}} = \dfrac{15}{25} \)
Simplify the expression:
\( \sin(\theta) = 0.6 \)
Now, find the angle using the inverse sine function:
\( \theta = \sin^{-1}(0.6) \)
Using a calculator or reference table, the angle is:
∴ θ ≈ 36.9°
4. A ramp is installed to provide access to a stage. If the ramp is 10 meters long and rises 6 meters vertically, what is the angle of the ramp with the horizontal?
Answer
Given:
- Length of the hypotenuse (ramp) = 10 meters
- Length of the adjacent side (rise) = 6 meters
First, calculate the sine of the angle:
\( \sin(\theta) = \dfrac{\text{rise}}{\text{length of ramp}} = \dfrac{6}{10} \)
Simplify the expression:
\( \sin(\theta) = 0.6 \)
Now, find the angle using the inverse sine function:
\( \theta = \sin^{-1}(0.6) \)
Using a calculator or reference table, the angle is:
∴ θ ≈ 36.9°