cos−1 Calculator
x= adjacent_side/hypotenuse
cos−1(x)
Calculating Inverse Cosine of a Value
The inverse cosine (cos⁻¹) function, also known as arccosine, is used to find the angle whose cosine is a given value. This function is particularly useful in trigonometry when you need to determine the angle based on the ratio of the adjacent side to the hypotenuse in a right-angled triangle.
The inverse cosine of a value \( x \) is defined as:
\( \theta = \cos^{-1}(x) \)
where:
- θ is the angle corresponding to the cosine value.
- x is the cosine value, representing the ratio of the adjacent side to the hypotenuse.
Consider the following triangle ABC, right-angled at vertex B.
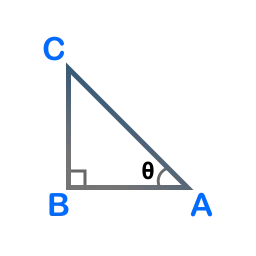
For the angle \( \theta \) at vertex A:
- Adjacent side = AB
- Hypotenuse = AC
Therefore,
\( \cos^{-1}(x) = \theta \) where \( x = \dfrac{\text{length of side AB}}{\text{length of side AC}} \)
Examples
The following examples demonstrate how to use the inverse cosine function to find the angle when the cosine value is known.
1. A ski lift forms an angle with the ground as it ascends a mountain. If the distance between the base of the lift and the top of the mountain is 200 meters (hypotenuse), and the horizontal distance covered is 150 meters (adjacent side), what is the angle of elevation of the ski lift?
Answer
Given:
- Length of the hypotenuse (lift path) = 200 meters
- Length of the adjacent side (horizontal distance) = 150 meters
First, calculate the cosine of the angle:
\( \cos(\theta) = \dfrac{\text{horizontal distance}}{\text{length of lift path}} = \dfrac{150}{200} \)
Simplify the expression:
\( \cos(\theta) = 0.75 \)
Now, find the angle using the inverse cosine function:
\( \theta = \cos^{-1}(0.75) \)
Using a calculator or reference table, the angle is:
∴ θ ≈ 41.4°
2. An engineer is designing a ramp that must ascend to a platform. The ramp's length is 10 meters (hypotenuse), and it needs to cover a horizontal distance of 8 meters (adjacent side). What is the angle that the ramp makes with the ground?
Answer
Given:
- Length of the hypotenuse (ramp) = 10 meters
- Length of the adjacent side (horizontal distance) = 8 meters
First, calculate the cosine of the angle:
\( \cos(\theta) = \dfrac{\text{horizontal distance}}{\text{length of ramp}} = \dfrac{8}{10} \)
Simplify the expression:
\( \cos(\theta) = 0.8 \)
Now, find the angle using the inverse cosine function:
\( \theta = \cos^{-1}(0.8) \)
Using a calculator or reference table, the angle is:
∴ θ ≈ 36.9°
3. A road signpost is leaning towards the road. The height of the post is 4 meters (adjacent side), and the distance from the base of the post to the point where it touches the ground is 5 meters (hypotenuse). What is the angle at which the post is leaning?
Answer
Given:
- Length of the hypotenuse (post height when tilted) = 5 meters
- Length of the adjacent side (original post height) = 4 meters
First, calculate the cosine of the angle:
\( \cos(\theta) = \dfrac{\text{height of post}}{\text{length of tilted post}} = \dfrac{4}{5} \)
Simplify the expression:
\( \cos(\theta) = 0.8 \)
Now, find the angle using the inverse cosine function:
\( \theta = \cos^{-1}(0.8) \)
Using a calculator or reference table, the angle is:
∴ θ ≈ 36.9°
4. A cyclist is descending a hill. If the distance traveled downhill is 30 meters (hypotenuse) and the horizontal distance covered is 24 meters (adjacent side), what is the angle of descent?
Answer
Given:
- Length of the hypotenuse (downhill path) = 30 meters
- Length of the adjacent side (horizontal distance) = 24 meters
First, calculate the cosine of the angle:
\( \cos(\theta) = \dfrac{\text{horizontal distance}}{\text{length of downhill path}} = \dfrac{24}{30} \)
Simplify the expression:
\( \cos(\theta) = 0.8 \)
Now, find the angle using the inverse cosine function:
\( \theta = \cos^{-1}(0.8) \)
Using a calculator or reference table, the angle is:
∴ θ ≈ 36.9°