csc−1 Calculator
x= hypotenuse/opposite_side
csc−1(x)
Calculating Inverse Cosecant of a Value
The inverse cosecant (cosec⁻¹) function, also known as arccosecant, is used to find the angle whose cosecant is a given value. This function is useful in trigonometry when you need to determine the angle based on the ratio of the hypotenuse to the opposite side in a right-angled triangle.
The inverse cosecant of a value \( x \) is defined as:
\( \theta = cosec^{-1}(x) \)
where:
- θ is the angle corresponding to the cosecant value.
- x is the cosecant value, representing the ratio of the hypotenuse to the opposite side.
Consider the following triangle ABC, right-angled at vertex B.
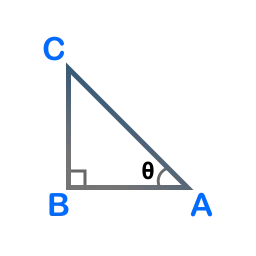
For the angle \( \theta \) at vertex A:
- Hypotenuse = AC
- Opposite side = BC
Therefore,
\( cosec^{-1}(x) = \theta \) where \( x = \dfrac{\text{length of side AC}}{\text{length of side BC}} \)
Examples
The following examples demonstrate how to use the inverse cosecant function to find the angle when the cosecant value is known.
1. A ladder leans against a wall, making a steep angle. The length of the ladder is 13 feet, and the height at which it touches the wall is 5 feet. What is the angle between the ladder and the ground?
Answer
Given:
- Length of the hypotenuse (ladder) = 13 feet
- Length of the opposite side (height) = 5 feet
First, calculate the cosecant of the angle:
\( cosec(\theta) = \dfrac{\text{length of ladder}}{\text{height}} = \dfrac{13}{5} \)
Simplify the expression:
\( cosec(\theta) = 2.6 \)
Now, find the angle using the inverse cosecant function:
\( \theta = cosec^{-1}(2.6) \)
Using a calculator or reference table, the angle is:
∴ θ ≈ 22.6°
2. A kite string is stretched tightly and measures 25 meters in length. The kite is flying at a height of 7 meters above the ground. What is the angle of elevation of the string from the ground?
Answer
Given:
- Length of the hypotenuse (string) = 25 meters
- Length of the opposite side (height) = 7 meters
First, calculate the cosecant of the angle:
\( cosec(\theta) = \dfrac{\text{length of string}}{\text{height}} = \dfrac{25}{7} \)
Simplify the expression:
\( cosec(\theta) \approx 3.57 \)
Now, find the angle using the inverse cosecant function:
\( \theta = cosec^{-1}(3.57) \)
Using a calculator or reference table, the angle is:
∴ θ ≈ 16.2°
3. A rope is tied from the top of a 10-meter-high pole to a point on the ground 24 meters away from the base of the pole. What is the angle of elevation of the rope?
Answer
Given:
- Length of the hypotenuse (rope) = 24 meters
- Length of the opposite side (pole height) = 10 meters
First, calculate the cosecant of the angle:
\( cosec(\theta) = \dfrac{\text{length of rope}}{\text{pole height}} = \dfrac{24}{10} \)
Simplify the expression:
\( cosec(\theta) = 2.4 \)
Now, find the angle using the inverse cosecant function:
\( \theta = cosec^{-1}(2.4) \)
Using a calculator or reference table, the angle is:
∴ θ ≈ 24.6°
4. A zip line is installed between two trees. The length of the zip line is 50 meters, and the difference in height between the two ends of the line is 20 meters. What is the angle of descent of the zip line?
Answer
Given:
- Length of the hypotenuse (zip line) = 50 meters
- Length of the opposite side (height difference) = 20 meters
First, calculate the cosecant of the angle:
\( cosec(\theta) = \dfrac{\text{length of zip line}}{\text{height difference}} = \dfrac{50}{20} \)
Simplify the expression:
\( cosec(\theta) = 2.5 \)
Now, find the angle using the inverse cosecant function:
\( \theta = cosec^{-1}(2.5) \)
Using a calculator or reference table, the angle is:
∴ θ ≈ 23.6°